Starting A Knot Project

I have begun work on a project where I will digitally represent, manipulate, and render the mathematical knots explored by the mathematical discipline known as knot theory.

Unlike the knots we most commonly encounter in real life, knots in knot theory are connected at both ends. For example, a knot known as a trefoil(the simplest knot) appears as this:

We may represent these knots digitally in a form known as extended Gauss code.

To construct the extended Gauss code of a knot, we first label each point in the knot with a unique integer id greater than 0.

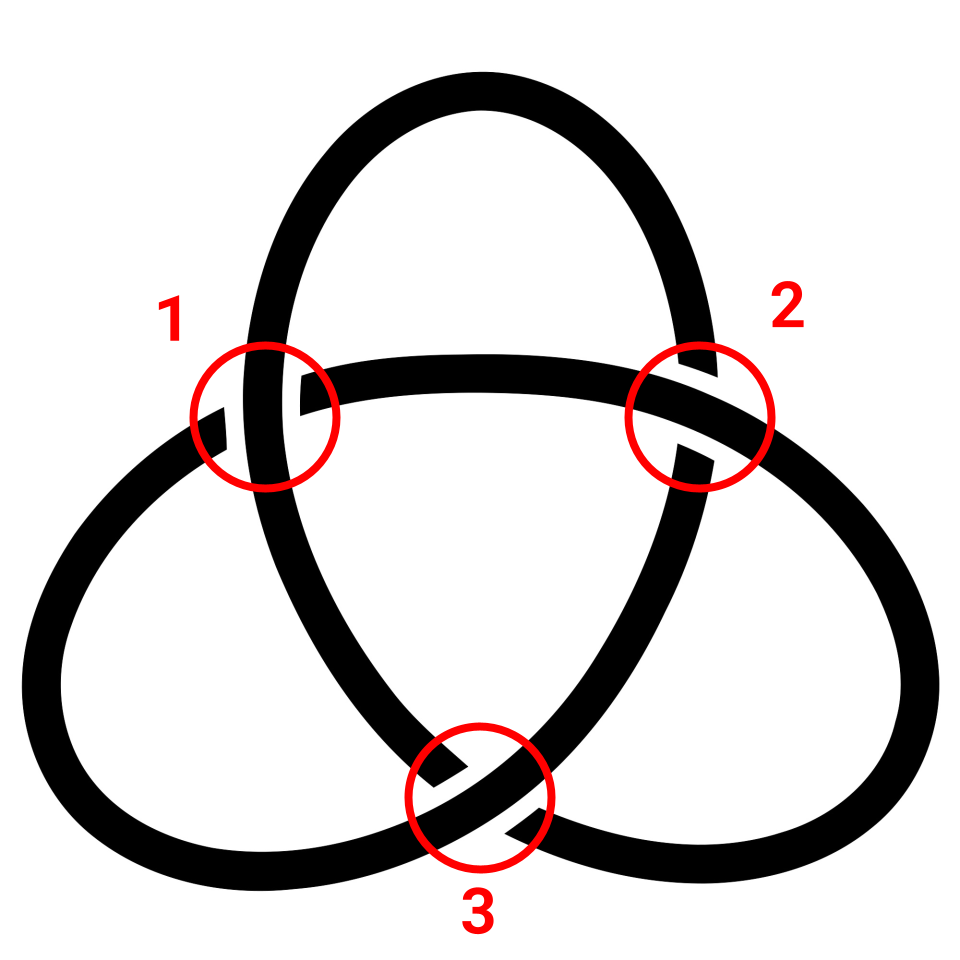
We then pick an arbitrary point on the knot, and an arbitrary direction to trace the “string” in.

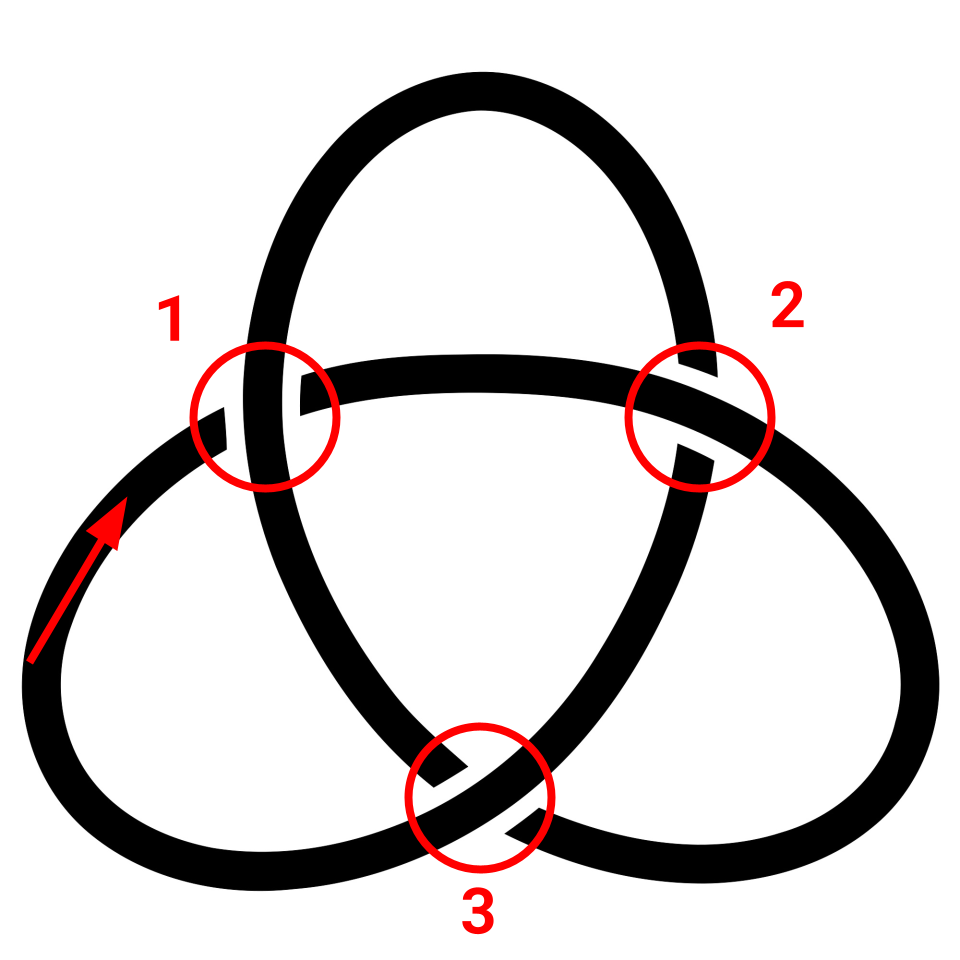
The first time we meet a particular crossing on the knot, we concatenate the knot’s id to the gauss code. But if it’s an under crossing, we instead concatenate the NEGATIVE id.

The second time we meet a particular crossing, we concatenate the knot’s id again. But this time the sign is determined by whether the under-crossing crosses from the right side of the over-crossing,(when the diagram is oriented such so that the over crossing points upwards) or from the left side. These are referred to as right-handed and left-handed crossings respectively.

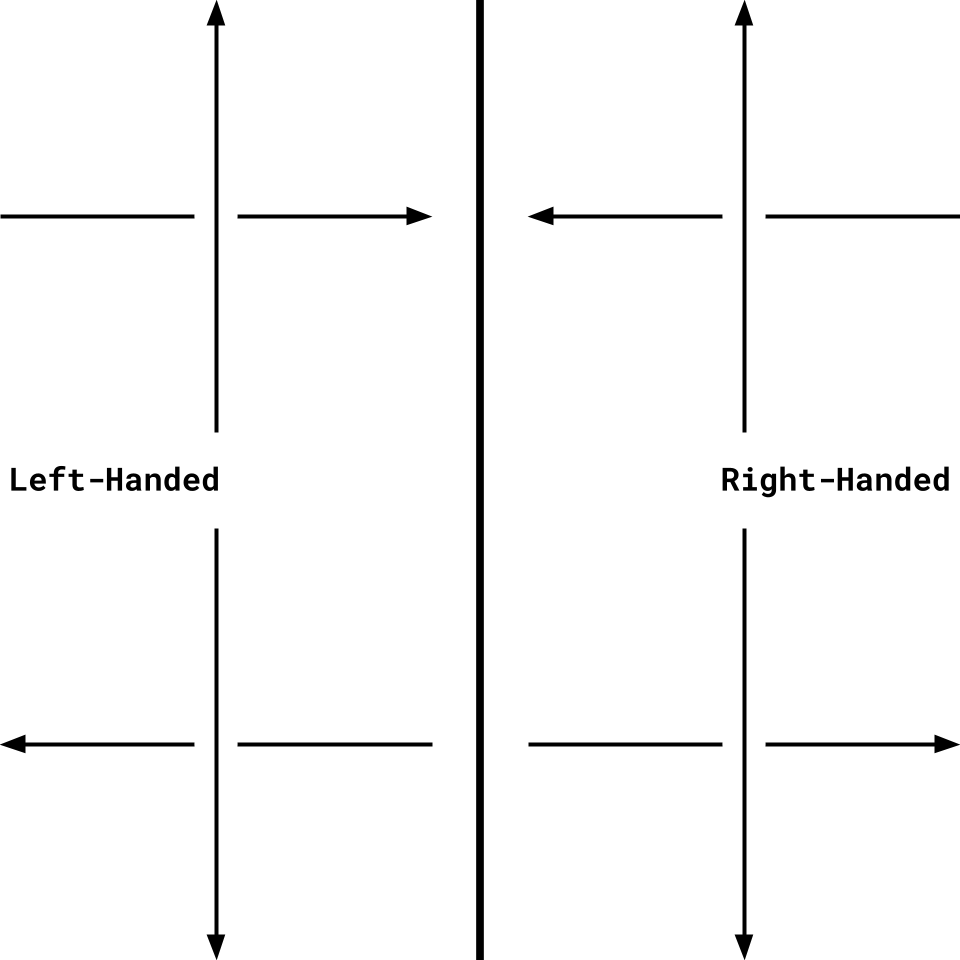
But manipulating Gauss code is difficult to debug without a visual aid, which is why the first part of this project I will tackle is rendering the knots.